Correlation Test
Q→Q is different in the sense that both variables are quantitative, and therefore, as you’ll discover, this case will require a different kind of treatment and tools.
Let’s start with an example:
Highway Signs
A Pennsylvania research firm conducted a study in which 30 drivers (of ages 18 to 82 years old) were sampled, and for each one, the maximum distance (in feet) at which he/she could read a newly designed sign was determined. The goal of this study was to explore the relationship between a driver’s age and the maximum distance at which signs were legible, and then use the study’s findings to improve safety for older drivers. (Reference: Utts and Heckard, Mind on Statistics (2002). Originally source: Data collected by Last Resource, Inc, Bellfonte, PA.)
Since the purpose of this study is to explore the effect of age on maximum legibility distance,
- the explanatory (X) variable is Age, and
- the response (Y) variable is Distance
Here is what the raw data looks like:
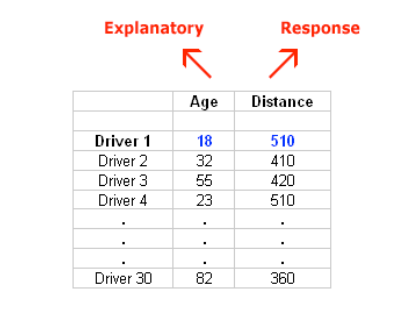
Note that the data structure is such that for each individual (in this case driver 1….driver 30) we have a pair of values (in this case representing the driver’s age and distance). We can therefore think about these data as 30 pairs of values: (18, 510), (32, 410), (55, 420), … , (82, 360).
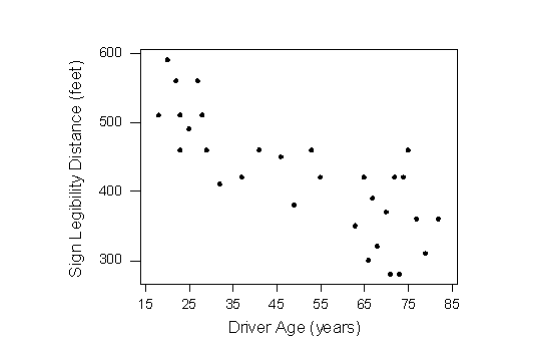
The first step in exploring the relationship between driver age and sign legibility distance is to create an appropriate and informative graphical display. The appropriate graphical display for examining the relationship between two quantitative variables is the scatterplot. Here is what the scatterplot looks like for this data:
Interpreting the Scatterplot
How do we explore the relationship between two quantitative variables using the scatterplot? What should we look at, or pay attention to?
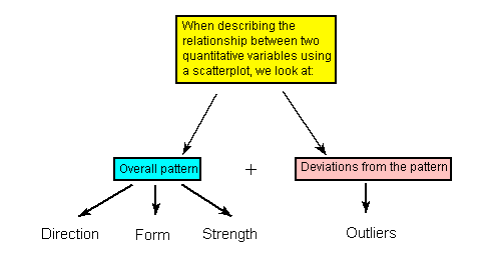
Recall that when we described the distribution of a single quantitative variable with a histogram, we described the overall pattern of the distribution (shape, center, spread) and any deviations from that pattern (outliers). We do the same thing with the scatterplot. The following figure summarizes this point:
As the figure explains, when describing the overall pattern of the relationship we look at its direction, form and strength.
The direction of the relationship can be positive, negative, or neither:
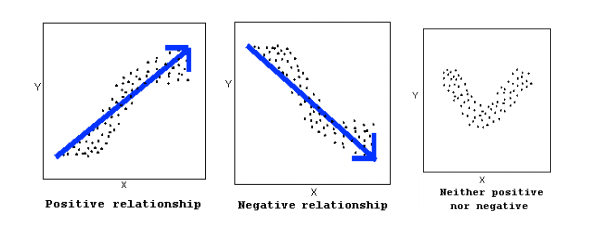
A positive (or increasing) relationship means that an increase in one of the variables is associated with an increase in the other.
A negative (or decreasing) relationship means that an increase in one of the variables is associated with a decrease in the other.
Not all relationships can be classified as either positive or negative.
The form of the relationship is its general shape. When identifying the form, we try to find the simplest way to describe the shape of the scatterplot. There are many possible forms. Here are a couple that are quite common:
Relationships with a linear form are most simply described as points scattered about a line:
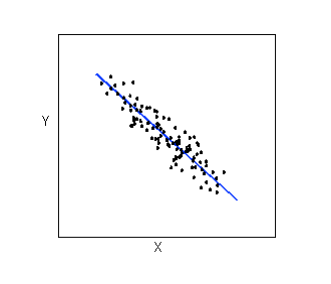
Relationships with a curvilinear form are most simply described as points dispersed around the same curved line:
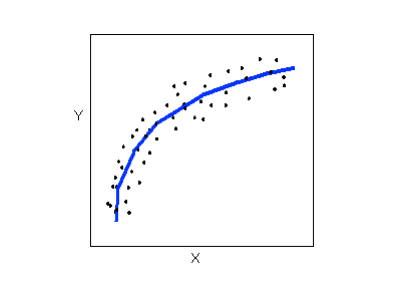
There are many other possible forms for the relationship between two quantitative variables, but linear and curvilinear forms are quite common and easy to identify. Another formrelated pattern that we should be aware of is clusters in the data:
The strength of the relationship is determined by how closely the data follow the form of the relationship. Let’s look, for example, at the following two scatterplots displaying positive, linear relationships:
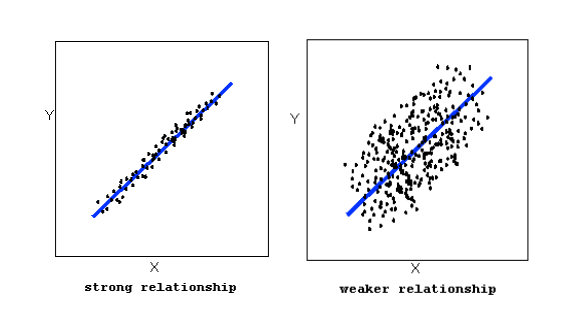
The strength of the relationship is determined by how closely the data points follow the form. We can see that in the top scatterplot the data points follow the linear pattern quite closely. This is an example of a strong relationship. In the bottom scatterplot, the points also follow the linear pattern, but much less closely, and therefore we can say that the relationship is weaker. In general, though, assessing the strength of a relationship just by looking at the scatterplot is quite problematic, and we need a numerical measure to help us with that. We will discuss that later in this section.
Data points that deviate from the pattern of the relationship are called outliers. We will see several examples of outliers during this section. Two outliers are illustrated in the scatterplot below:
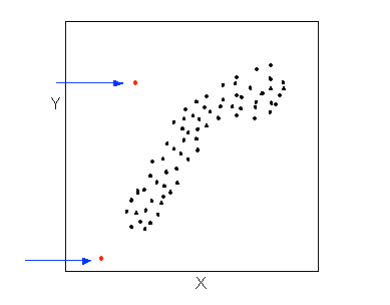
Let’s go back now to our example, and use the scatterplot to examine the relationship between the age of the driver and the maximum sign legibility distance. Here is the scatterplot:
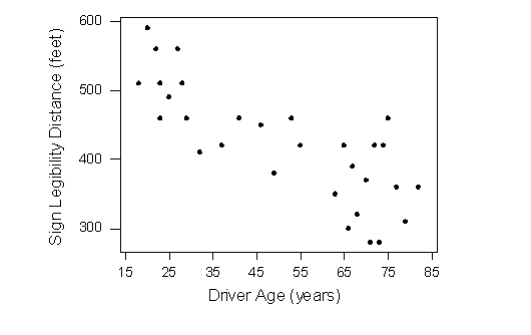
The direction of the relationship is negative, which makes sense in context, since as you get older your eyesight weakens, and in particular older drivers tend to be able to read signs only at lesser distances. An arrow drawn over the scatterplot illustrates the negative direction of this relationship:
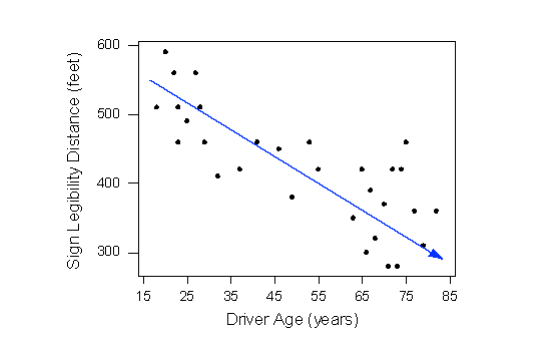
The form of the relationship seems to be linear. Notice how the points tend to be scattered about the line. Although, as we mentioned earlier, it is problematic to assess the strength without a numerical measure, the relationship appears to be moderately strong, as the data is fairly tightly scattered about the line. Finally, all the data points seem to “obey” the pattern—there do not appear to be any outliers.
The Correlation Coefficient—r
The numerical measure that assesses the strength of a linear relationship is called the correlation coefficient, and is denoted by r. We will:
- give a definition of the correlation r
- discuss the calculation of r,
- explain how to interpret the value of r, and
- talk about some of the properties of r
Definition: The correlation coefficient (r) is a numerical measure that measures the strength and direction of a linear relationship between two quantitative variables.
Calculation: r is calculated using the following formula:
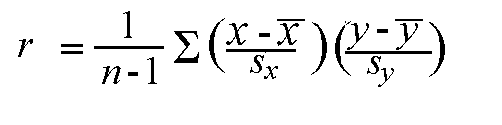
However, the calculation of the correlation (r) is not the focus of this course. We will use a statistics package to calculate r for us, and the emphasis of this course will be on the interpretation of its value.
Interpretation and Properties: Once we obtain the value of r, its interpretation with respect to the strength of linear relationships is quite simple, as this walkthrough will illustrate:

Highway Sign Visibility
Earlier, we used the scatterplot below to find a negative linear relationship between the age of a driver and the maximum distance at which a highway sign was legible. What about the strength of the relationship? It turns out that the correlation between the two variables is r = -0.793.
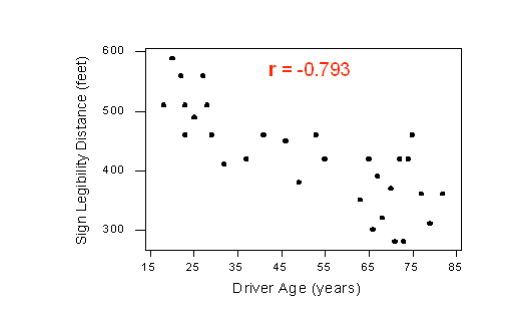
Since r < 0, it confirms that the direction of the relationship is negative (although we really didn’t need r to tell us that). Since r is relatively close to -1, it suggests that the relationship is moderately strong. In context, the negative correlation confirms that the maximum distance at which a sign is legible generally decreases with age. Since the value of r indicates that the linear relationship is moderately strong, but not perfect, we can expect the maximum distance to vary somewhat, even among drivers of the same age.
Statistics Courses
A statistics department is interested in tracking the progress of its students from entry until graduation. As part of the study, the department tabulates the performance of 10 students in an introductory course and in an upper-level course required for graduation. What is the relationship between the students’ course averages in the two courses? Here is the scatterplot for the data:
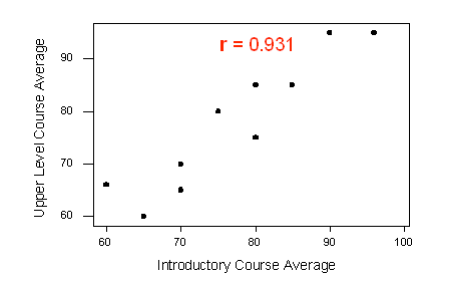
The scatterplot suggests a relationship that is positive in direction, linear in form, and seems quite strong. The value of the correlation that we find between the two variables is r = 0.931, which is very close to 1, and thus confirms that indeed the linear relationship appears very strong.
Assessment of r in a hypothesis test
Now that we can interpret the correlation coefficients that we obtain, we will want to know whether the correlation coefficients indicate a significant linear relationship.
The hypotheses we are testing are:
- H0: There is no linear relationship between X and Y (r=0)
- Ha: There is a linear relationship between X and Y (r≠0)
As before, a small p-value will suggest that there is enough evidence to reject the null hypothesis. This will suggest that there is a significant linear relationship between X and Y. The output of a correlation test will typically produce the sample correlation coefficient (r), the test-statistic (t), and the p-value.
Example:
Suppose we would like to examine the relationship between IQ score and GPA. We begin by examining the following plot:
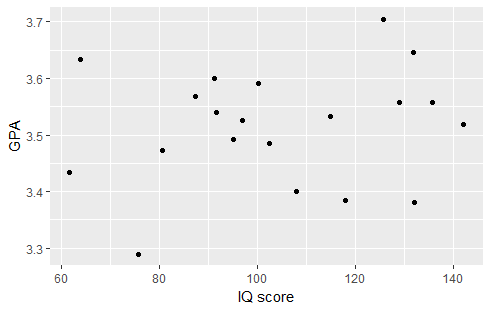
There appears to be a very slight positive relationship between the two variables. Therefore, it was not surprising to find a correlation coefficient of r=0.1746. Testing the relationship we find the following output:

The correlation coefficient r=0.1746 is not significantly different from 0 (t=0.7523, p-value=0.4615). Therefore, there is not enough evidence to suggest that there is a linear relationship between IQ score and GPA.
Please watch the following video (Correlation)
Correlation
-
R
-
SAS
-
Stata
-
Python
Watch Correlation Lessons 1-3 (Videos 29-31 on Playlist)
Pre-Class Quiz
After reviewing the material above, take Quiz 9 in moodle. Please note that you have 2 attempts for this quiz and the higher grade prevails.
During Class Tasks
Mini-Assignment 6
Project Component H: click here
